Theory

The hyperfine splitting of atomic energy levels—so named because it occurs on a scale several orders of magnitude smaller (μeV-meV) than that of the “fine structure” spin-orbital interaction— is due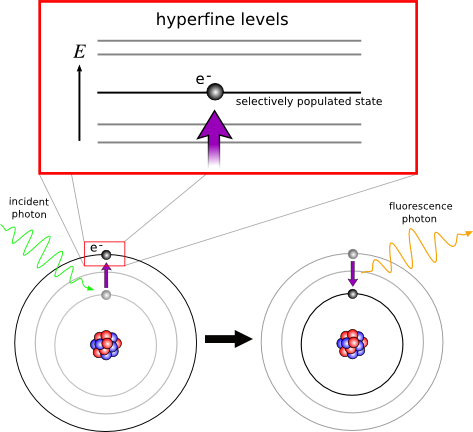 to perturbations of the orbitals of atomic orbitals caused by interactions with the internal structure of the nucleus. One can therefore study certain properties of an atom's nucleus, such as its charge radius, magnetic dipole and electric quadrupole moments, by making precise measurements of its electrons' hyperfine energy transitions. Laser spectroscopy accomplishes this by using a tunable laser to selectively populate a hyperfine state in the atom of interest. When the laser is tuned at the appropriate transition frequency, the atom will undergo resonance excitation into the desired state. After a short time the state decays, releasing its energy in the form of fluorescence. By measuring the intensity of this fluorescence while slowly varying the frequency of incident photons, we can determine the frequency of maximum resonance, and therefore the precise energy level of a hyperfine state.

Several different interactions contribute to the hyperfine structure of any given atom. The inherent overall spin of the nucleus, characterized by the quantum number I, creates a magnetic dipole moment μ_I which interacts with the orbital electrons in a way that depends on their total (spin plus orbital) angular momentum (characterized by the quantum number J). For given fixed values of I and J, the number of multiplet states corresponds to the number of possible values for F—the total angular momentum quantum number. These can run from F = I + J to F = |I - J|, so the number of states that the atom can occupy is given by (2I + 1) or (2J + 1), whichever is smaller. These multiplets will have distinct strengths of magnetic interaction due to differing angular momenta, resulting in a splitting of the macroscopic energy level into as many distinct hyperfine levels as there are multiplet states. States for which I and J are both greater than ½ will also be perturbed by the electric quadrupole moment Q_s which arises from any deformation in the charge distribution of the nucleus. Thus, measuring the spacing of hyperfine levels allows us to determine both the shape of the nucleus and its magnetic moment.

When comparing the spectra of two isotopes of the same element, one finds a shift in the central frequency from one isotope to the next.

This is known as the isotope shift, and is comprised of  several distinct factors:

The first term is the normal mass shift,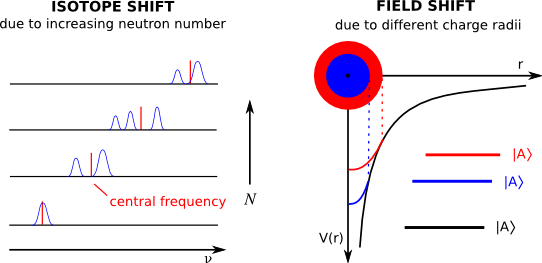 caused by the change in the reduced mass due to the addition or removal of a neutron from the nucleus, and can be easily calculated and accounted for if the masses of both isotopes are known to sufficient precision. The specific mass shift results from correlations between electron positions in a multi-electron atom, and is somewhat more difficult to calculate. Once these two effects—which together comprise the total mass shift—are accounted for, the remaining contribution to the isotope shift is due to a third term, the field shift (also known as the volume shift), which is caused by the deviations of the nucleus' electric field from that of a pure Coulomb potential. It is this field shift term which is of principal interest, since it is proportional to the mean square charge radius. This quantity is important since it is affected both by the size and the deformation of the nucleus.